Optimización

Optimización

Objetivo

Resolución de ejercicios de optimización

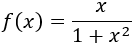
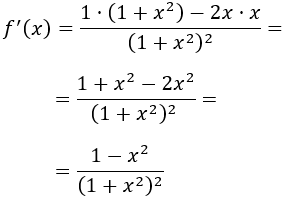
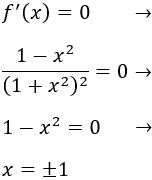
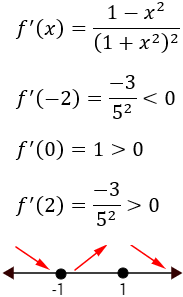
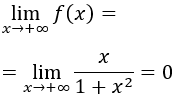
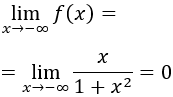
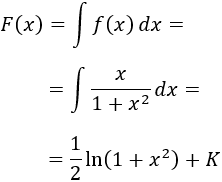
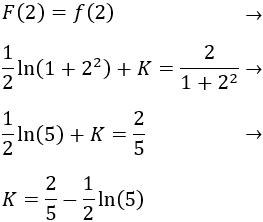
Ejemplo 1

Encontrar los extremos relativos y absolutos (si los hay) de la función

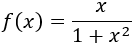
y obtener una función $F\left(x\right)$ primitiva de $f$ tal que $F\left(2\right)=f\left(2\right)$.

Solución:

Calculamos la derivada de $f$ para buscar sus extremos:

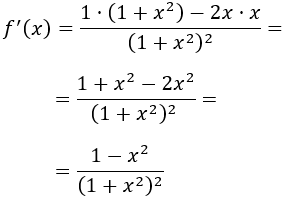
Igualamos a 0 la derivada y resolvemos la ecuación para encontrar los puntos críticos:

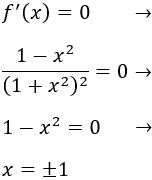
Representamos los puntos críticos en la recta real y estudiamos el signo de la derivada en los intervalos que determinan:

Utilizaremos los valores $x=\pm 2$ y $x=0$:

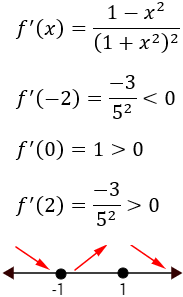
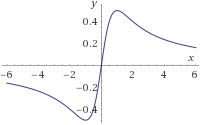
Por tanto, $f$ es decreciente cuando $x\le 1$ y $x\ge 1$ y creciente cuando $-1<x<1$. Deducimos entonces que $f$ tiene un mínimo en $x=-1$ y un máximo en $x=1$.

Como la función decrece en el intervalo $x\le -1$ hasta llegar al mínimo, no puede haber valores de $f$ que sean menores que el mínimo $x=-1$ en dicho intervalo.

La función crece en el intervalo $-1<x<1$ desde el mínimo, así que tampoco puede tomar valores menores que el mínimo.

Sin embargo, la función decrece en el intervalo $x\ge 1$, así que sí puede haber valores menores que el mínimo si decrece indefinidamente.

El límite de la función es

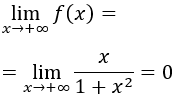
Hay una asíntota vertical en $y=0$ y el mínimo es $f(-1)=-0.5$. Como el mínimo toma un valor menor que la asíntota, es un mínimo absoluto.

Razonando del mismo modo, la función sólo podría tomar valores mayores que el máximo ($f\left(1\right)=1/2$) en el intervalo $x\le -1$. Pero esto no se da puesto que hay una asíntota en $y=0$:

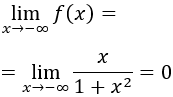
Gráfica:

Para obtener una primitiva $F$ de $f$, integramos $f$:

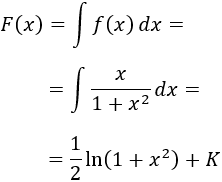
Buscamos la constante $K$ para que $F\left(2\right)=f\left(2\right)$:

Aquí les dejo la resolución del problema

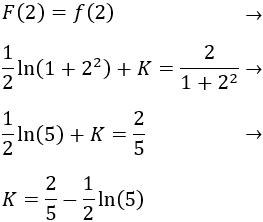
Ejemplo 2

La función

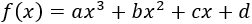
tiene un extremo en $x=\pm 1$ y

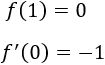
Calcular los coeficientes $a,b,c$ y $d$ y determinar si los extremos proporcionados son mínimos o máximos.

Solución:

Evaluando $f$ en $x=1$ obtenemos una ecuación:

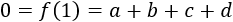
Calculamos la derivada de $f$:

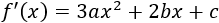
Evaluando la derivada en $x=0$ obtenemos que $c=-1$:

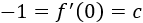
Luego la derivada de $f$ es

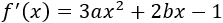
Sabemos de la existencia de dos extremos, así que la derivada se anula en dichos extremos:

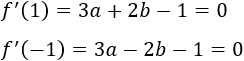
Sumando estas dos últimas ecuaciones podemos calcular el valor del coeficiente $a$:

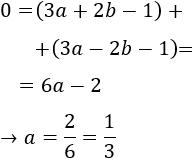
Sustituyendo en cualquiera de las dos ecuaciones anteriores se obtiene $b=0$.

Finalmente, utilizamos la primera ecuación obtenida:

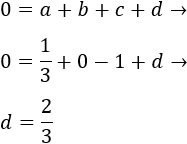
Los coeficientes son

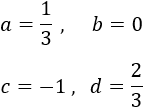
Y la función es

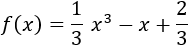
Como sólo queremos saber el tipo de dos extremos en concreto, usaremos el criterio de la segunda derivada.

Calculamos la segunda derivada:

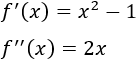
Evaluamos los puntos críticos::

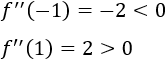
Por tanto, el extremo $x=-1$ es un máximo y $x=1$ es un mínimo.

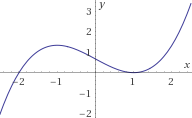
La gráfica de la función es

Aquí les dejo la resolución del problema