Optimización
Objetivo
Resolución de ejercicios de optimización
Ejemplo 1
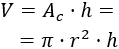
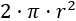
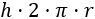
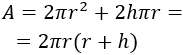
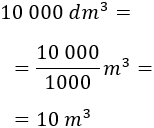
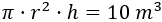
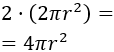
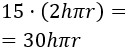
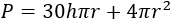
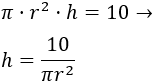
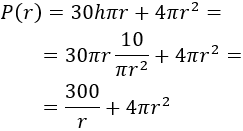
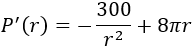
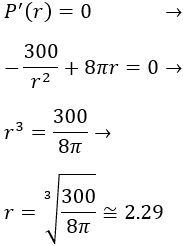
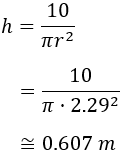
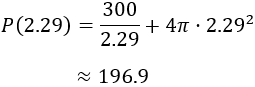
Para fabricar un depósito cilíndrico de agua se necesitan materiales distintos para las bases y el lateral. El precio por metro cuadrado del material de las bases es de $2 y el del lateral es de $15.

Calcular la altura y el diámetro para que el coste de un depósito de 10 mil litros de capacidad sea mínimo. ¿Cuál es el precio del depósito?
solucion
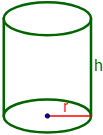
Tendremos que utilizar las fórmulas del área y del volumen de un cilindro. Sean el radio y su altura.
El volumen se calcula fácilmente multiplicando el área de la base (que es un círculo) por su altura:
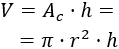
El área de la superficie es el área de las bases más el área del lateral. Como las bases son dos círculos de radio , sus áreas suman
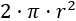
El lateral es un rectángulo de altura y cuya base coincide con el perímetro de la base del cilindro, así que su área es
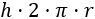
Por tanto, el área total del cilindro es
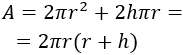
Como los precios de los materiales del cilindro son por metro cuadrado, la unidad de medida que utilizaremos será el metro.
La capacidad del cilindro debe ser 10000L. Sabiendo que un litro equivale a , la capacidad ha de ser de 10 000 . Es decir,
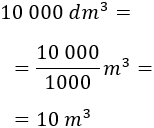
Igualamos el volumen del cilindro a su capacidad:
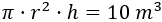
El precio del material es de $2 por metro cuadrado de base. Como hay dos bases, la cantidad asciende a
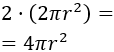
Y como el precio del lateral es de $15 por metro cuadrado, éste asciende a
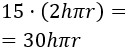
Luego la función precio del cilindro (del depósito) es
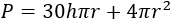
Podemos escribir en función de :
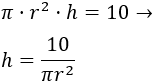
Así, la función es
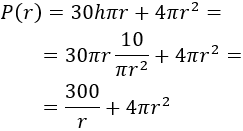
Derivamos la función:
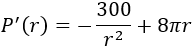
Igualamos a 0 y resolvemos la ecuación para encontrar los puntos críticos:
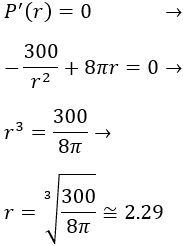
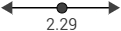
Representamos la recta real con el único punto crítico:

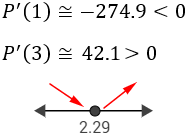
Ahora estudiamos el signo de la derivada en cada intervalo. Nosotros escogemos los puntos y :

Luego la función tiene un mínimo en .
Por tanto, el radio debe medir 2.29m y la altura
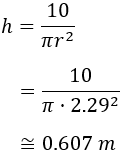
El precio del depósito nos lo proporciona la función:
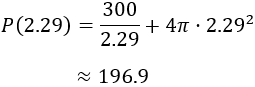
El precio del depósito es $196.9

disculpen en dónde me doy cuenta de que con las medidas que me dieron la capacidad es la mínima ?
ResponderBorrar