Optimización

Optimización

Objetivo

En esta parte del blog  le voy a explicar en que se puede usar la optimzación.

Para comenzar la optimización se utiliza para encontrar máximos y mínimos 

Ejemplo

Se quiere construir una caja sin tapa a partir de una hoja de cartón de 20x10cm. Para ello, se corta un cuadrado de lado L en cada esquina y se dobla la hoja levantando los cuatro laterales de la caja.

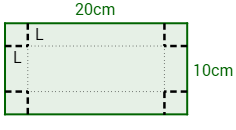
Determinar las dimensiones de la caja para que su volumen sea máximo si el lado $L$ debe medir entre 2 y 3 cm ($2\le L\le 3$).

Solución:

Si $a$ es el ancho de la caja, $h$ es su altura y $p$ es su profundidad, entonces su volumen es

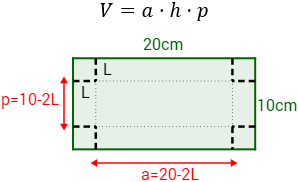
Al cortar los cuatro cuadrados de lado $L$, el ancho de la caja es

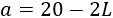
La profundidad es

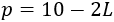
Por último, la altura coincide con el lado del cuadrado recortado:

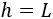
Luego el volumen de la caja en función de $L$ es (paso 1)

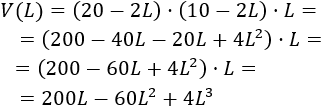
Derivamos la función volumen (paso 2):

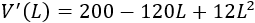
Igualamos a 0 la derivada y resolvemos la ecuación para encontrar los puntos críticos (paso 3):

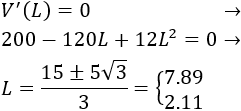
Situamos los puntos en la recta real y estudiamos los signos en los intervalos (paso 4):

Escogemos los puntos $x=1$ del primer intervalo, $x=3$ del segundo intervalo y $x=8$ del tercero:

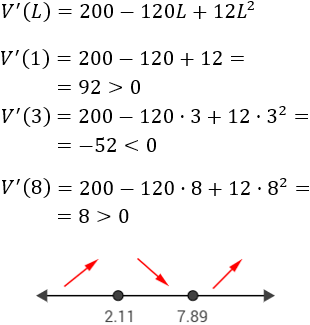
Luego la función es creciente en el primer intervalo, decreciente en el segundo y creciente en el tercero:

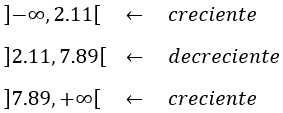
Pero el lado $L$ debe medir entre 2 y 3, es decir, debe ser

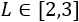
Como en el intervalo $[2.11,3]$ la función es decreciente, el volumen será máximo para $L=2.11cm$.

Por tanto, las dimensiones de la caja deben ser

Es decir, las dimensiones son 15.78 x 5.78 x 2.11 cm y su volumen es $192.45c{m}^2$.

Aquí les dejo la resolución del ejemplo